题目描述
给定一个后缀数组 Suffix Array 和词典大小(alphabet size),求总共有多少种不同的可能性。题目链接 1526 E
这道题的描述很简单,但思维量很大。官方 Solution 又写的非常简洁。忙了一个星期,我总算完成了这道题。
这道题可以拆分成两问
1. 给定后缀数组,使用最小的字典生成合法的字符串
对于非空的字符串 S 和对应的后缀数组 SA,我们有如下性质
- \( 0 \leq SA_i \leq n-1 \)
- SA is a permutation of
[0, n-1] - SA 对应的后缀字符串严格递增(lexical order)
- 对于本问,上界为 n, 下界为 1
根据后缀数组的定义,我们有
\[i < j \Leftrightarrow S[SA_i,n-1] < S[SA_j,n-1]\]我们将 \(S[SA_i,n-1]\) 拆成 \(xY\),\(x\) 表示一个合法的字符,\(Y\) 则表示一个可能为空的字符串。同理,将 \(S[SA_j,n-1]\) 拆分成 \(aB\),如下图
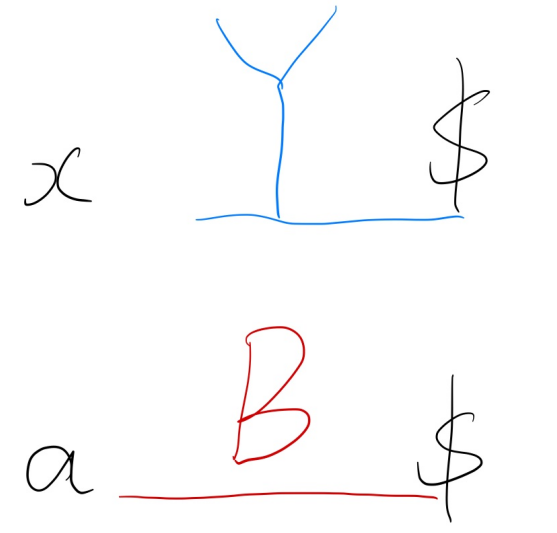
注意,在这里我们不清楚 \(Y B\) 的长度。因为 \(xY \neq aB\),可知\(Y \neq B\)
显然,在这里 \(x \leq a \). 想要使用尽可能小的字典, 我们希望尽可能地使用相同的字符。那么,我们能得到
- \(Y < B\ \Rightarrow x = a\)
- \(Y > B\ \Rightarrow x < a\)
当出现后者的情况时,我们就需要将一个新的字符插入字典,从而满足后缀数组 SA 的要求。因为 SA 是严格升序的, \(\forall i \in [0,n-2], j=i+1 \Rightarrow S[SA_i,n-1] < S[SA_j,n-1] \) 即可保证 SA 合法。
现在,我们需要高效地比较 \(Y B\)。因为后缀数组 SA 已知,这个问题非常简单。我们可以定义函数 Rank(U),表明对于字符串 S 的后缀 U在所有后缀中的排名。为了方便,我们定义空串 Rank($)=-1.
官方 Solution 使用了 pos 这一宽泛的名称,不易理解。OneInDark 的博文 准确地称之为 rnk,我也沿用了这一名词。
根据后缀数组的定义,我们可以使用下标 \(u\) 表示字符串 \(U = S[u, n-1]\). 那么,Rank(n)=-1. 这一问的代码实现如下:
fn calculate_strict_increasing_pairs(sa: &Vec<i32>) -> usize {
let mut rank = vec![0; sa.len()+1];
for i in 0..sa.len() {
rank[ sa[i] as usize ] = i as i32;
}
// rank[n] = -1
// means an empty string $ is lexicographically smaller than all non-empty strings
rank[sa.len()] = -1;
let mut cnt = 0;
for i in 0..(sa.len()-1) {
let j = i + 1;
// xY = [SAi, n-1]
// aB = [SAj, n-1]
// xY < aB
// if Y < B, x may be equal to a
let y:usize = sa[i] as usize + 1;
let b:usize = sa[j] as usize + 1;
if rank[y] < rank[b] {
()
} else {
cnt += 1;
}
}
cnt
}
这里的 cnt 指,为了满足要求我们需要多少次换用新的字符。也就是说,我们需要一个大小为 cnt+1 的字典。当且仅当 \(k<=cnt\) 时,不存在任何一个合法的字符串 S满足SA。
2. 隔板法(Stars and bars)求可行的方案数
定义非负整数数列 \(X\), 令 \(x_i=0\) 表示字符串 \(S\) 中 \(S_i = S_{i-1} \). 如果 \(x_i \geq 1\),那么 \(S_i\) 相比于 \(S_{i-1} \) 要向前推 \(x_i\) 个字符。这样我们将题目转化成了,数列 \(X\) 有多少种合法的可能。
定义一个由整数 \(0\) \(1\) 组成的数列 \(Y\). 如果第一问中 \(S_i > S_{i-1} \), 那么 \(y_i = 1\). 否则,\(y_i=0\). 数列 \(Y\) 仅由第一问中的 \(SA\) 确定。数列 \(X\) 合法的充要条件是 \(\forall i: x_i \geq y_i\)
定义非负整数数列 \(Z = X - Y\). 求数列 \(X\) 有多少种合法的可能性,等价于求数列 \(Z\) 有多少种合法的可能。
令 \(extra = k-1-cnt\), 表示我们有多少个额外的字母。 如果 \(cnt=k-1\),那唯一合法的数列 \(Z\) 为 \(\forall i: z_i = 0\),我们没有任何一个字母可以浪费。可以枚举 \(w \in [0, extra] \), 令 \(w = \sum Z\), 可以使用 隔板法(Stars and bars) Theorem Two 求解。
但是,枚举 \(w\) 效率过低。我们可以在 \(Z\) 的末尾添加一个元素,得到数列 \(Z^{\star}\). 这个额外元素的值表示 \(extra - w\). 那么,\( \sum Z^{\star} = extra\). 以 \(k = 26, n = 10\) 举例,如果我们希望字符串 \(S\) 的第一个元素是 c,我们就令 \(z_0^{\star} = 2\). 如果字符串 \(S\) 的第末尾元素是 y,我们就令 \(z^{\star}_{last} = 1\)
现在,我们就将前文的 枚举 \(w \in [0, extra] \) 转化为了使用 隔板法(Stars and bars) Theorem Two 求数列 \(Z^{\star}\) 的可能数。数列长度为 \(n+1\),数列和为 \( extra = k-1-cnt\). 答案要取余,这要用到 Modular multiplicative inverse 的知识。可以参考 Geeksforgeeks 的实现。
后记
官方 Solution 写的过于简洁。OneInDark 的博文 详细了不少,为我提供了很大的帮助。
写题解时发现了 \( \LaTeX \) 速查表,记录在此以备将来使用。
意外读到了 谢益辉 的博文: MathJax 与 Markdown 的究极融合,感觉当前自己的 Jekyll + MathJax 的组合的确不是很方便。未来可能会寻找一个更好的写作方法。
这道题目有两个主要的思维点,每一个都让我感觉很吃力。从前到后忙了得有一周,总算有了个比较圆满的结果。
最近我在尝试使用 Rust 打 Codeforces,欢迎大家提出建议。
