之前参加了 Codeforces Round #726，E2 这道题方法很多，推荐的方法是 Z Function. 我也借机学习一个新算法。

函数定义

本文中，所有的数组下标均为 0 开始。如无说明，所有的区间均为闭区间。对于字符串 S, S[a, b] 表示选取一个长度为 b - a + 1，范围是由 a 到 b 的子串。

函数 Z 的定义是，给定一个字符串 S. 对于每个下标 i，寻找一个最长的子串使 S[i,i+Zi - 1] = S[0, Zi - 1]. Z[0] 未被定义。如果 S[i] != S[0]，我们有 Z[i] = 0

直观一些的理解是，一个序列的前缀 (prefix) 在可能在这个序列中重复出现。例如，Open reading frame 中，特定的密码子会在碱基序列的起始和前端重复出现。Z-function 反应了重复出现的情况。

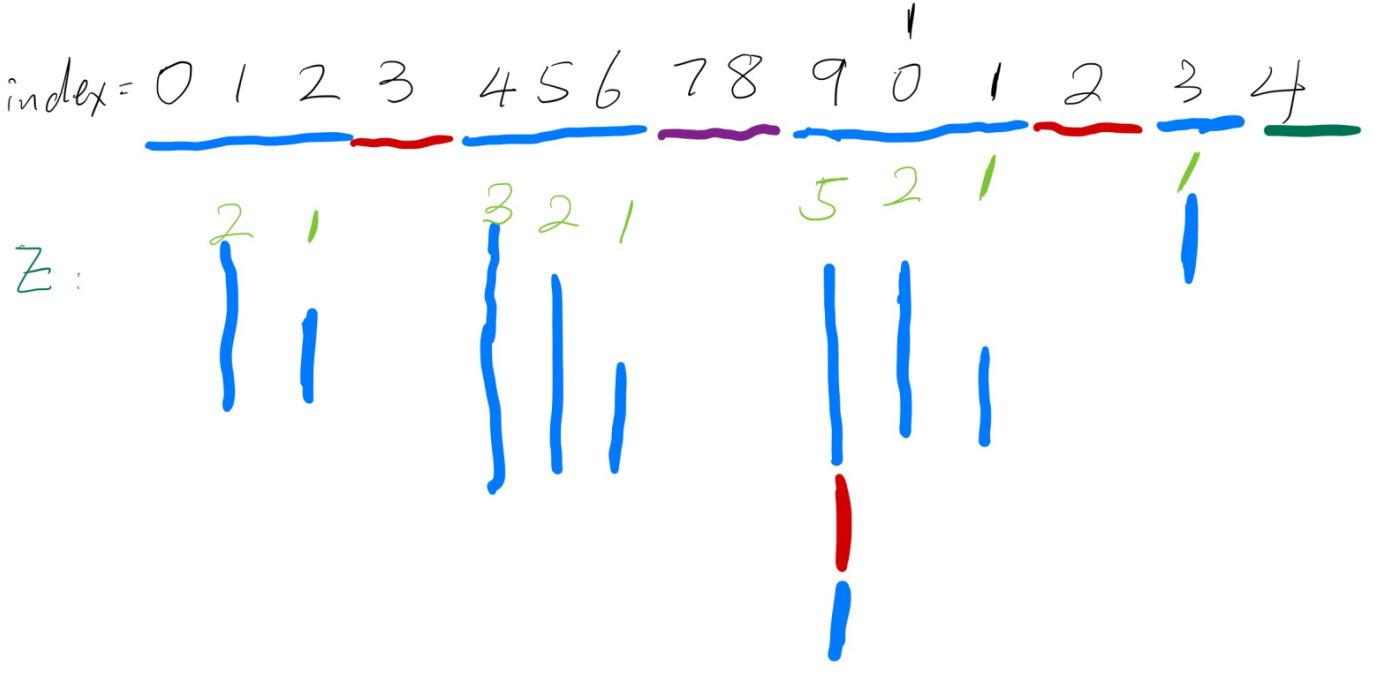
我手绘了一张示意图，相同颜色表示重复的元素。向下延伸的部分，表示 S[i, i+Zi - 1] = S[0, Zi - 1]，也就是与前缀重合的部分。

z-function-drawing

线性时间求解

根据定义，可以容易地写出一个 Brute-force 的算法，求出序列 S 对应的 Z. 但当序列 S 的前缀在序列中多次重复出现时，耗时会快速增加。极端情况下，aaaaa 这类序列，会达到 Brute-force 算法的最坏时间复杂度，O(n^2).

通常提到 Z Function 的时候，都是要在线性时间内求出结果。我们可以使用 Sliding Window Technique，维护一个与 S 的前缀相同的 window. 其范围是 [L, R] 。也就是说，这个 window:

  1. L > 0
  2. S[0, R - L] = S[L, R]

L 与 R 均保持递增，易证算法的时间复杂度为 O(n)

求 Z[i] 时，

  1. 若 i > R，则这个 window 没有为我们提供已知的信息。令 L = R = i，再向右尽可能地延伸 R
  2. 若 i <= R，我们将 S[L, R] 拆分成 S[L, i] 和 S[i, R] (有意重叠S[i])
    • 令 k = i - L. 因为 S[0, R-L] = S[L, R]， 我们可证 S[0, k] = S[L, i]。
    • 同理，S[k, R - L] = S[i, R]. 这样，我们就用上了 window 内的信息。
    • 如果 Z[k] < R - i + 1 ，就说明在子串 S[k, R - L] 中存在 p >= Z[k], 使 S[k+p] != S[0+p]。 这也就是说， S[i+p] != S[p]。同样，对于任意 q < Z[k]，我们有 S[i+q] = S[k+q] = S[q]。因此，Z[i] = Z[k]
    • 如果 Z[k] >= R - i + 1，我们在保持 L 不变的基础上，尽可能延伸 R

使用 C++ 实现如下

void extend_window(const char *str, int str_len, int left, int &right) {
    // S[0:right-left] == S[left:right]   closed interval
    // if S[0] != S[right], resulting in  left+1==right, indicating an empty range
    while (right < str_len && str[right - left] == str[right]) {
        ++right;
    }
    --right;
}
void z_function(const char *str, int str_len, int Z[]) {
    Z[0] = 0;
    int left = -1;
    int right = -1;
    for (int i=1; i < str_len; ++i) {
        if (i > right) {
            left = right = i;
            extend_window(str, str_len, left, right);
            Z[i] = right - left + 1;
        } else {
            int k = i - left;
            // We know S[0:right-left]  ==  S[left:right] =>
            //      1. S[0:k]           ==  S[left:i]
            //      2. S[k, right-left] ==  S[i:right]
            if (Z[k] < right - i + 1) {
                // exist p>=0, S[k+p] != S[p] => S[i+p] != S[p]
                Z[i] = Z[k];
            } else {
                left = i;
                extend_window(str, str_len, left, right);
                Z[i] = right - left + 1;
            }
        }
    }
}

UT Dallas CS 6333 提供了一个直观的网页演示。

后记

介绍 Z Function 的英文文章不少，但我个人感觉 HackerEarth 的描述最为清晰。

Z Function 的英文定义可以参考 CMU 295 z-string-matching Page 7

e-maxx 提供了若干道例题，如 Codeforces - Password. Codechef 的教程也举出了两道例题。

resilar 提供了更为精简的实现。

UT Dallas 的课程页面 和 Matteo Dunnhofer 的文章 都提到了 Gusfield, Dan. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology. 但我手头并没有这本书，并没有验证 Gusfield 的书上是否提到了这一算法。

非常感谢 ITX351 对本文提供的宝贵意见。